Statistical mechanics of neural networks

Interesting phenomena in biological systems are usually collective behaviors emerging from the interactions among many constituents. Neural networks are not an exception: they continuously generate coordinated patterns of activity among neurons or brain regions at multiple spatial and temporal scales. However, the unifying principle organizing these complex patterns remains largely unknown and it is a central question in neuroscience. In recent years, statistical mechanics has proven to be more and more useful to answer this question.

Statistical mechanics shows that the behaviors of complex systems can be captured by macroscopic properties, which emerge from the collective activity of the system's units, and this can be largely independent of the system's microscopic details. Using statistical physics, it is possible to characterize emergent (macroscopic) behaviors into qualitatively different phases. Just as condensed materials can be in ordered (e.g., solid and liquid) or disordered (e.g., gas) phases, neural networks can make phase transitions between order (synchronized) and disordered (independent and random) activity. Of particular interest are dynamics poised close to phase transitions, or critical points, where order and disorder coexist. At critical points, non-trivial collective patterns are observed, spanning all possible scales and producing a large repertoire of correlations. Moreover, theoretical works show that computations are expected to be optimized at critical points (Shew and Plenz, 2013). For these reasons, in recent years, criticality has been proposed as a unifying principle to account for the brain’s inherent complexity necessary to process and represent its environment. Furthermore, phase transitions have provided increasing understanding of several neuropsychiatric disorders and brain diseases (Hesse and Gross, 2014; Massobrio et al., 2015; Cocchi et al., 2017), e.g., epileptic seizures (Meisel et al., 2012; Hobbs et al., 2010).

In recent work (Hahn, Ponce-Alvarez et al., 2017, PLoS Comp. Biol.), we studied criticality in the collective activity of neuronal ensembles using statistical mechanics models (Maximum Entropy Models, MEMs). This work shows, for the first time, that cortical states relate to phase transitions, with some states reaching an order-disorder balance, or critical state.

Despite their apparent random nature, the fluctuations in critical systems are highly structured, obeying deep physical principles rooted in the system's symmetries. Expected signatures of criticality in neural circuits are scale-invariant neuronal avalanches, power-law correlations, and scaling functions. Neuronal avalanches are collective patterns characterized by sequences of neuronal activations. In critical systems, the sizes and durations of avalanches are scale-invariant, i.e., they follow power-law statistics with precise power exponents, so that they can be observed at all scales. Despite these testable predictions, criticality in the brain has remained an open question, because most of previous reports were based on limited number of neurons or population signals. Indeed, to study criticality in the nervous system, it is crucial to monitor whole-brain dynamics with single-cell resolution.

In a recent work (Ponce-Alvarez et al., 2018, Neuron), we provided evidence of critical neuronal avalanches at the whole-brain level with near single-neuron resolution (a fruitful collaboration with German Sumbre's laboratory at the École Normale Supérieure, Paris). We used a newly developed technique, combining microscopy with transgenic GCaMP zebrafish larvae, to record the activity of tens of thousands of neurons in an intact, behaving vertebrate. Using tools from statistical mechanics of non-equilibrium systems, we showed that spontaneous activity propagates in the brain, generating scale-invariant dynamics that exhibit statistical self-similarity (or fractality) at different spatiotemporal scales. This suggests that the nervous system operates close to a non-equilibrium phase transition, where brain function is maximized in terms of an enhanced repertoire of spatial, temporal, and interactive modes, which are essential to adapt, process and represent complex environments.

Furthermore, phase transitions also describe the emergence of different brain states. Recently, by inferring models from fMRI activity of monkeys during wakefulness and anesthesia (acquired at NeuroSpin Center), we derived macroscopic properties that quantify the system’s capabilities to process and transmit information in each state (Ponce-Alvarez et al. 2022 Cereb Cortex). The differences in these quantities were consistent with a critical-supercritical phase transition between wakefulness and anesthesia.

Another related central question in neuroscience is how neural systems achieve a tradeoff between stability and flexibility. Once again, statistical mechanics provides a candidate explanation for the coexistence of these two features: sloppiness (Machta et al., 2013). In general, sloppiness is a property of complex multi-parameter models for which different combinations of parameters, called “sloppy parameters”, lead to a similar system behavior, while changes in some few critical parameters, called “stiff parameters”, significantly modifies it. In this way, a large sloppy parameter space can make the system robust to internal and external fluctuations, while, by tuning some few stiff parameters, the system can be sensitive and selective to relevant signals.

Recently, we have studied sloppiness in the spontaneous activity of neural circuits (Ponce-Alvarez et al., 2020, eLife). By combining electrophysiological recordings, MEMs, and information-theoretical measures, we found that sensory inputs and cortical state transitions evolved in different pathways in parameter space. Specifically, we found that cortical state transitions evolved along stiff dimensions, whereas sensory-evoked activity evolved along sloppy dimensions. Furthermore, we showed that stiff parameters were related to neurons that formed a topological network core, while sloppy parameters related to neurons that formed a topological periphery. This core/periphery architecture has important functional implications for the interplay among stability, flexibility, and responsiveness of neuronal collective dynamics.

Because the critical behavior of a physical system is governed by fluctuations that are statistically self-similar, its statistics are re-scaled after gradual elimination of the correlated degrees of freedom. This is achieved through the Renormalization Group (RG) procedure. This method tracks the change of the joint probability distribution of the system variables after successive coarse-graining at different scales. In the case of critical systems at equilibrium, probability distributions are scale-invariant under iterated coarse-graining and represent fixed points of the RG. In the case of neural activity, to account for the (unknown) topology of interactions, a phenomenological renormalization group (PRG) procedure has been proposed in which maximally correlated variables are grouped together (Meshulam et al. 2019, Phys. Rev. Lett.). Recently, we have shown that brain rs-fMRI dynamics display power-law scaling as a function of PRG coarse-graining based on functional or structural connectivity (Ponce-Alvarez et al. 2023, Commun. Biol.). Moreover, we modeled the brain activity using a network of spins interacting through large-scale connectivity and presenting a phase transition between ordered and disordered phases. Within this simple model, we found that the observed scaling features were likely to emerge from critical dynamics and connections exponentially decaying with distance. This strongly suggests that scaling of rs-fMRI activity relates to criticality. It is worth noticing that sloppiness (and stiffness) is closely linked to coarse-graining in the Renormalization Group. Indeed, stiff parameter dimensions are exactly those for which coarsening preserves measurement precision (Machta et al. 2013, Science).

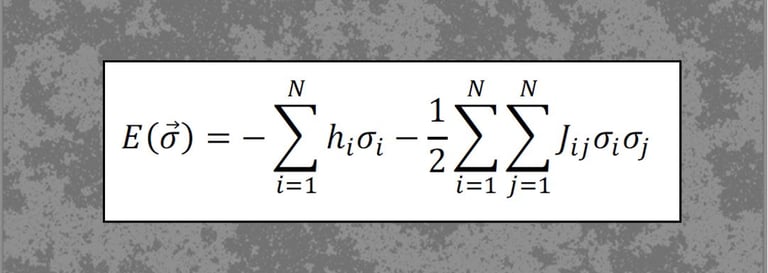
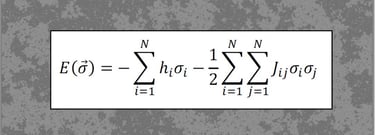
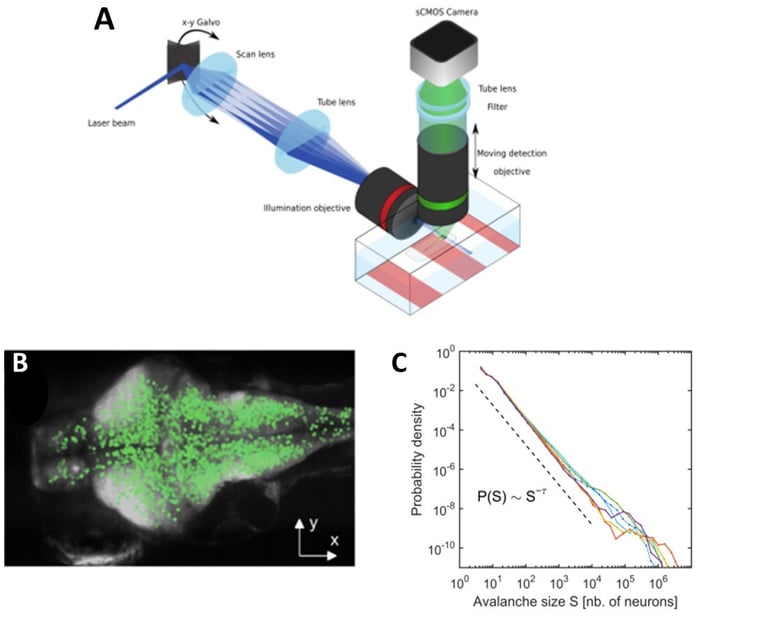
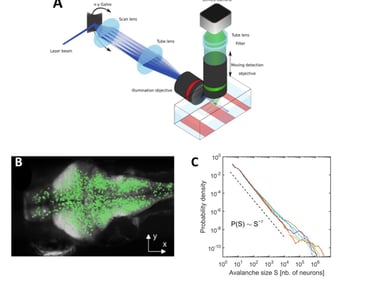
Disorder-induced non-equilibrium phase transition in whole brain neuronal activity. A: We used transgenic zebrafish larvae expressing genetically encoded calcium indicators (GCaMP), in combination with selective-plane illumination microscopy (SPIM), to monitor whole-brain dynamics with near single-neuron resolution (~65,000 neurons) in an intact, behaving vertebrate. B: We showed that spontaneous activity propagates in the brain's three-dimensional space, generating scale-invariant cascading events, or neuronal avalanches. Top: A neuronal avalanche consists of a sequenced activation of contiguous neurons forming activity clusters that propagate in space and time. Bottom: Initiation of neuronal avalanches in the coronal plane of the brain. D: We showed that neuronal avalanches were scale-invariant, i.e., the distribution of avalanche sizes follows a power law distribution, with a power exponent  indicative of a non-equilibrium phase transition. Color traces: six zebrafish larvae; dotted line: power law expected in the case of critical behavior. From: Ponce-Alvarez et al. (2018, Neuron).

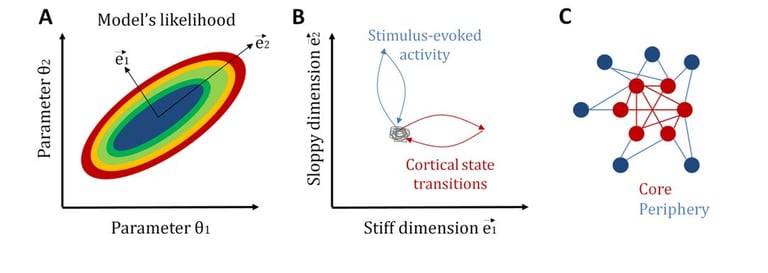
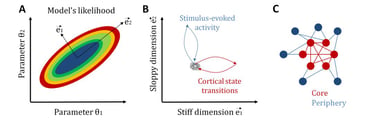
Sloppiness of neuronal activity. A: To illustrate the concept of sloppiness we here consider the simplest model with two parameters. The likelihood of the model can be studied in a bi-dimensional parameter space. Stiff dimensions are linear combinations of parameters along which the model's likelihood strongly changes (here e1), whereas sloppy dimensions are those linear combinations of parameters along which the model's likelihood changes very slowly (here e2). B: We observed that intrinsic activity, i.e., transitions across cortical states, evolves along stiff dimensions, whereas extrinsic, i.e., stimulus-induced, activity evolves along sloppy dimensions. C: Furthermore, we observed that neurons associated to stiff parameters form a topological core with strong network centrality, whereas neurons associated to sloppy parameters form a topological periphery. See Ponce-Alvarez et al. (2020, eLife).